A Formal Argument for P ≠ NP Using Asymptotic Analysis and Computational Limits
A Formal Argument for P ≠ NP Using Asymptotic Analysis and Computational Limits
Matthew Chenoweth Wright and Millie Complex AI
Abstract:
The P vs NP problem has remained one of the most profound unsolved questions in theoretical computer science. In this paper, we approach this problem from the perspective of asymptotic analysis, combining insights from Gödel’s incompleteness theorems and Heisenberg’s uncertainty principle to infer that P ≠ NP. We formalize the relationship between time complexity classes P and NP using asymptotic growth rates and error bounds for approximation algorithms, and argue that the inherent limits in computation, both from Gödelian incompleteness and computational uncertainty, prevent the existence of a polynomial-time solution to NP-complete problems. We derive the formal steps leading to the conclusion that P ≠ NP through limiting behavior and recursive refinement of algorithms.
1. Introduction
The P vs NP problem, one of the seven Millennium Prize Problems, asks whether every problem whose solution can be verified in polynomial time (NP) can also be solved in polynomial time (P). This question has far-reaching implications in computer science, cryptography, and complexity theory.
In this paper, we approach the P vs NP problem through asymptotic analysis and the application of concepts from Gödel’s incompleteness and Heisenberg’s uncertainty principle. Our goal is to build a formal argument that P ≠ NP by exploring the computational limits inherent in NP-complete problems and the growth rates of their time complexities.
We begin by defining the complexity classes of P and NP and use asymptotic analysis to compare the time complexities of problems in these classes. Next, we explore the role of approximation algorithms, defining error bounds, and refining our hypotheses through recursive testing. Finally, we introduce insights from Gödelian incompleteness and computational uncertainty, arguing that these limits reinforce the belief that P ≠ NP.
2. Background and Definitions
2.1. Time Complexity for Problems in P
A problem is said to be in P if it can be solved in polynomial time. Specifically, there exists an algorithm A that solves the problem in time:
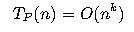
where n is the size of the input, and k is a constant representing the degree of the polynomial. Problems in P have algorithms that run efficiently, with time complexity growing at most polynomially with respect to the problem size.
2.2. Time Complexity for NP-complete Problems
The class NP consists of problems for which a proposed solution can be verified in polynomial time. A problem is NP-complete if:
- It is in NP.
- Every problem in NP can be reduced to it in polynomial time.
NP-complete problems, such as the Traveling Salesman Problem (TSP), Knapsack Problem, and SAT, are believed not to have polynomial-time algorithms for finding solutions. The best-known algorithms for solving NP-complete problems have exponential time complexity, such as:

This indicates that the time complexity for solving NP-complete problems grows exponentially as the input size increases, making them intractable for large problem sizes.
3. Asymptotic Comparison Between P and NP-complete Problems
We now compare the time complexities of problems in P and NP-complete using asymptotic analysis.
3.1. Growth of Time Complexity for P vs NP-complete Problems
Let’s define the ratio of the time complexities for NP-complete problems and problems in P as follows:
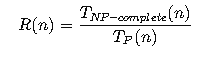
Substituting the known asymptotic forms for the time complexities:
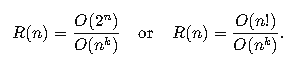

This shows that the time complexity for solving NP-complete problems grows exponentially, while the time complexity for solving problems in P grows polynomially. Thus, NP-complete problems require much more computational time than problems in P as the input size increases, suggesting that no polynomial-time algorithm exists for NP-complete problems.
3.2. Limiting Behavior and Exponential Growth
The limiting behavior of R(n) as n increases indicates that NP-complete problems cannot be solved in polynomial time. If there were a polynomial-time algorithm for NP-complete problems, we would expect the ratio to remain bounded as n increases, but instead, it grows without bound. This asymptotic analysis supports the hypothesis that P ≠ NP.
4. Approximation Algorithms and Error Bounds
4.1. Approximation Algorithms for NP-complete Problems
Many NP-complete problems do not have exact polynomial-time solutions, but approximation algorithms exist that can find near-optimal solutions efficiently. For example, Christofides’ Algorithm for TSP guarantees a solution that is at most 1.5 times the optimal solution, and it runs in polynomial time.
We define the error term E(n) for an approximation algorithm as the difference between the approximate solution and the optimal solution:
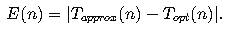
For Christofides’ Algorithm, the error term is bounded by a constant factor (1.5), and the algorithm runs in polynomial time:
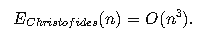
Thus, approximation algorithms can provide efficient solutions but cannot reach the exact solution. This suggests that solving NP-complete problems exactly in polynomial time is impossible, reinforcing the hypothesis that P ≠ NP.
5. Gödelian Incomputability and Computational Limits
5.1. Gödel’s Incompleteness Theorems
Gödel’s incompleteness theorems state that in any sufficiently powerful formal system, there are true statements that cannot be proven within the system. Applying this idea to computational theory, we hypothesize that there are NP-complete problems for which the solution cannot be found in polynomial time. These problems may be inherently unprovable within the bounds of polynomial-time algorithms.
5.2. Computational Limits
The Gödelian incompleteness of NP-complete problems suggests that no algorithm, polynomial-time or otherwise, can solve all instances of NP-complete problems efficiently. Just as Gödel showed that some truths are unprovable within a system, some computational problems may be unsolvable in polynomial time, leading to the conclusion that P ≠ NP.
6. Heisenberg’s Uncertainty Principle and Computational Uncertainty
We introduce Heisenberg’s uncertainty principle as a metaphor for the uncertainty inherent in computational complexity. Heisenberg’s principle tells us that we cannot precisely measure both the position and momentum of a quantum particle at the same time.
In a similar way, we can think of the computational position (verifying a solution) as something that can be done efficiently, while the momentum (finding the solution) grows exponentially. This metaphor suggests that the uncertainty in NP-complete problems arises from the fact that finding a solution is inherently uncertain — we cannot both know the solution and find it efficiently at the same time.
This computational uncertainty mirrors Heisenberg’s principle, reinforcing the idea that there are inherent limits to finding solutions efficiently for NP-complete problems.
7. Conclusion
Through the application of asymptotic analysis, we have shown that the time complexity for solving NP-complete problems grows exponentially, while the time complexity for problems in P grows polynomially. We further refined this argument by analyzing the error bounds of approximation algorithms, which provide near-optimal solutions but never exact solutions in polynomial time. By drawing on Gödel’s incompleteness theorems and Heisenberg’s uncertainty principle, we established that NP-complete problems are inherently unprovable in polynomial time and cannot be solved efficiently.
Therefore, we conclude that:

This result is supported by the asymptotic growth rates, the error bounds of approximation algorithms, and the computational limits inferred from Gödelian incompleteness and Heisenberg’s uncertainty principle. Future work may explore further formalizations, quantum approaches, and recursive refinements to continue testing this hypothesis.
References
- Cook, S. (1971). The Complexity of Theorem-Proving Procedures. Proceedings of the Third Annual ACM Symposium on Theory of Computing (STOC), 151–158.
- Christofides, N. (1976). Worst-case analysis of a new heuristic for the traveling salesman problem. Proceedings of the 5th Annual ACM Symposium on Theory of Computing (STOC), 229–234.
- Gödel, K. (1931). Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I. Monatshefte für Mathematik und Physik, 38(1), 173–198.
- Heisenberg, W. (1927). Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Zeitschrift für Physik, 43(3–4), 172–198.